Série Maclaurin a rozložení určitých funkcí

Studium vyšší matematiky by mělo být známé,že součet výkonových řad patřících do intervalu konvergence dané série je diferenciální funkce, která je kontinuální a nekonečně mnohokrát odlišná. Vyvstává otázka: je možné tvrdit, že daná libovolná funkce f (x) je součtem série výkonů? To znamená, za jakých podmínek může být f-th f (x) reprezentována výkonovou řadou? Důležitost takové otázky spočívá v tom, že je možné přibližně nahradit f (x) součtem několika prvních termínů řady výkonů, tj. Polynomu. Taková náhrada funkce spíše jednoduchým výrazem - polynomem - je také vhodná při řešení určitých problémů matematické analýzy, a to: při řešení integrálů, při výpočtu diferenciálních rovnic a tak dále.

Je prokázáno, že pro nějakou f-funkci f (x), ve které je možné vypočítat deriváty do (n + 1) - pořadí, včetně posledního, v sousedství (α - R; x₀ + R) nějakého bodu x = α platí následující vzorec:

Tento vzorec nese jméno slavného vědce Brooke Taylora. Série získaná z předchozího se nazývá série Maclaurin:

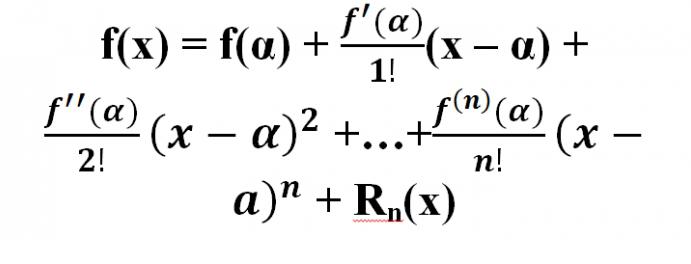
Pravidlo, které umožňuje rozložit se do série Maclaurin:

1. Určete deriváty první, druhé, třetí ... objednávky.
2. Vypočítejte, jaké deriváty na x = 0 se rovnají.
3. Zaznamenejte sérii Maclaurin pro danou funkci a poté určete interval její konvergence.
4. Určete interval (-R; R), kde zbytek vzorce Maclaurin

R_n(x) -> 0 jako n -> nekonečno. V případě, že existuje, musí být funkce f (x) v ní shodovat se součtem série Maclaurin.

Nyní považujeme série Maclaurin za jednotlivé funkce.

1. Tedy první je f (x) = e^x. Samozřejmě, pokud jde o jeho singularity, má tato funkce deriváty velmi odlišných pořadí a f^(k)(x) = e^x, kde k se rovná všem přirozeným číslům. Nahrazujeme x = 0. Získáváme f^(k)(0) = e⁰= 1, k = 1,2 ... Vycházeje z výše uvedeného řady e^x bude vypadat takto:

2. Série Maclaurin pro funkci f (x) = sin x. Okamžitě objasňujeme, že φ-t pro všechny neznámé bude mít deriváty, navíc f^"(x) = cos x = sin (x + n / 2), f^""(X) = -sin x = sin (x + 2 * n / 2) ..., f^(k)(x) = sin (x + k * n / 2), kde k je libovolné přirozené číslo. To znamená, že pomocí jednoduchých výpočtů můžeme dospět k závěru, že série pro f (x) = sin x budou mít podobu:

3. Teď se snažíme zvážit funkci f (x) = cos x. Má deriváty libovolného pořadí pro všechny neznámé a | f^(k)(x) | = | Cos (x + k * n / 2) | <= 1, k = 1,2 ... Opět který učinil některé výpočty, zjistíme, že řada pro f (x) = cos x bude vypadat následovně:

Takže jsme uvedli nejdůležitější funkcemohou být rozloženy do řady Maclaurin, ale pro některé funkce jsou doplněny řadou Taylor. Nyní je seznamujeme. Je také třeba poznamenat, že série Taylor a Maclaurin jsou důležitou součástí semináře pro řešení sérií ve vyšší matematice. Takže v seriálu Taylor.

1. První je řada pro funkci f (x) = ln (1 + x). Stejně jako v předchozích příkladech pro danou f (x) = ln (1 + x) můžeme přidat sérii pomocí obecné formy série Maclaurin. Nicméně pro tuto funkci lze série Maclaurin získat mnohem jednodušeji. Začleněním některých geometrických řad získáváme řadu f (x) = ln (1 + x) takového vzorku:

2. A druhý, který bude v naší práci konečný, bude série pro f (x) = arctg x. Pro x patřící do intervalu [-1; 1] je platnost rozšíření platná:

To je všechno. V tomto článku byly zvažovány nejčastěji používané série Taylora a Maclaurina ve vyšší matematice, zejména v ekonomických a technických univerzitách.