Co je integrální a jaký je jeho fyzický význam
Vzhled konceptu integrálu byl způsobennutnost nalézt antiderivující funkci s ohledem na její derivát, stejně jako určení množství práce, oblast složitých čísel, ujetá vzdálenost, s parametry načrtnutými křivkami popsanými nelineárními vzorci.
Z kurzu
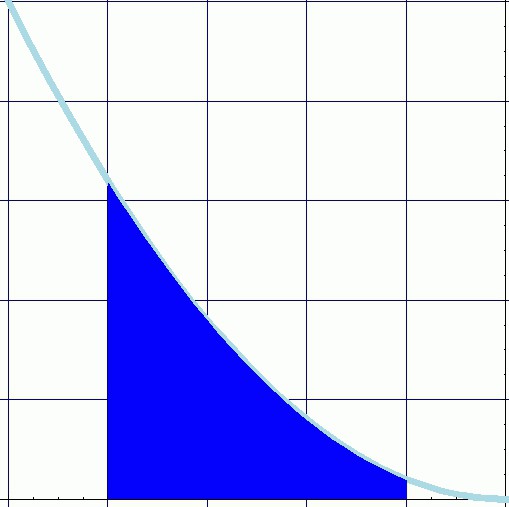
Ale síla se může měnit v průběhu práce a nějakou přirozenou závislostí. Stejná situace nastává při výpočtu ujeté vzdálenosti, pokud rychlost není konstantní.
Takže je jasné, proč je integrální. Definování to jako součet produktů hodnot funkce na nekonečně přírůstek argumentu zcela popisuje hlavní význam tohoto pojmu, jak se na oblast obrázku ohraničené horním řádku funkce, a okraje - vymezení hranic.
Jean Gaston Darboux, francouzský matematik, vdruhá polovina století XIX velmi jasně vysvětlila, co je integrální. Udělal to tak jasně, že celkově není pro žáky středních škol těžké pochopit tuto otázku.
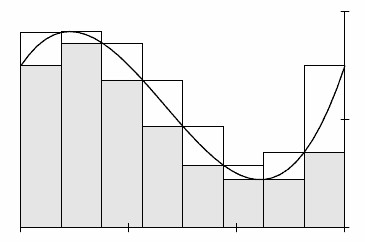
Předpokládejme, že existuje nějaká složitá funkce. y-osa, na které jsou uloženy na hodnotu argumentu, je rozdělen do malých intervalech, v ideálním případě, že jsou nekonečně malé, ale proto, že pojem nekonečna je zcela abstraktní, stačí si představit, jen malé kousky, je množství, které je obvykle označován řeckým písmenem delta (delta).
Funkce byla "řezána" do malých cihel.
Ke každé hodnotě argumentu odpovídá bodosa souřadnic, na které jsou vyneseny odpovídající hodnoty funkce. Ale vzhledem k tomu, že hranice vybrané části jsou dvě, pak budou hodnoty funkce také dvě, větší a menší.
Součet produktů s velkými hodnotami naPřírůstek Δ je nazýván velkou sumou Darboux a je označen jako S. V důsledku toho menší hodnoty na ohraničené části násobené Δ spolu tvoří malou součinnost Darboux. Sekce sama připomíná obdélníkový lichoběžník, protože zakřivení funkční linie může být zanedbáváno nekonečně malým přírůstkem. Nejjednodušší způsob, jak najít oblast takového geometrického tvaru, je přidání produktů větší a menší hodnoty na přírůstek Δ a rozdělit na dva, tj. Definovat jej jako aritmetický průměr.
Jedná se o integrál Darboux:
s = Σf (x) Δ je malá částka;
S = Σf (x + Δ) Δ je velká částka.
Takže, co je integrální? Oblast ohraničená funkční čárou a hranice definice budou:

∫f (x) dx = {(S + s) / 2} + c
To znamená, že aritmetický průměr velkých a malých součtů Darboux je konstantní hodnota, která je zrušena diferenciací.
Vychází z geometrického vyjádření tohotokoncept, fyzický význam integrálu je jasný. Plocha postavy, vymezená funkcí rychlosti a ohraničená časovým intervalem podél úsečky, bude délkou procházející cesty.
L = ∫f (x) dx v intervalu od t1 do t2,
Kde
f (x) je funkce rychlosti, tj. vzorec, kterým se mění s časem;
L je délka cesty;
t1 - čas začátku cesty;
t2 je koncový čas cesty.
Přesně podle stejného principu je určena velikost díla, pouze na podélné ose bude vzdálenost vykreslena a na souřadnici velikost síly aplikovaná v každém jednotlivém bodě.






