Praktická aplikace a nalezení inverzní matice

Matrix je tabulka, která je vyplněnaurčitou sadu čísel v určitém pořadí. Tento termín uvedl do oběhu významný anglický teoretik James Sylvester. Je jedním ze zakladatelů teorie uplatnění těchto matematických prvků.

K dnešnímu dni našli široké uplatněnípři provádění různých výpočtů, které jsou postaveny na základě takové metody, jako je například nalezení inverzní matice v různých odvětvích lidské činnosti. Tato metoda je založena na stanovení neznámých parametrů systému různých rovnic a je často používána při provádění ekonomických výpočtů.

Existují následující konkrétní případy datmatematické komponenty: malá, sloupec, nula, čtverec, diagonální, jednotlivá. Malá písmena tvoří pouze jeden řádek prvků a sloupec 1 sestává z jednoho sloupce čísel. Zero - všechny jeho prvky se rovnají 0. Na čtverci takového matematického prvku se počet sloupců rovná počtu řádků. Naopak u diagonálních prvků umístěných na hlavní diagonále se liší od "0" a zbytek v něm by se měl rovnat "0". Jeden - jedná se o jeden z poddruhů diagonální matice. Na hlavním úhlopříčku má pouze "1".

Příklady matric:

kde:_k Je obecný termín, a_ij - prvky,

(a) -2-rád;

b) - malými písmeny;

(c) -3-rád;

(r) je příklad jednotkové tabulky druhého řádu;

Existuje také inverzní matice, definicecož je následující. Když vynásobíte původní obrácenou tabulku, získá se jedna. Byla vyvinuta řada metod, které zajišťují nalezení inverzní matice. Nejjednodušší z nich je založeno na definici algebraických doplňků a determinantu (někdy se také nazývá determinant).

Determinant matice je výrazem a₁₁a₂₂-a₁₂a_21, označuje se takto:. Výše uvedený vzorec platí pro tabulku odpovídající druhému pořadí. Existují vzorce pro determinanty matic vyššího řádu. Povinnou podmínkou pro existenci determinantu je, že tabulka musí být čtvercová. V praxi se tento prvek této teorie nejčastěji používá v takovém postupu jako nalezení inverzní matice.

Druhou důležitou složkou, kterou můžeme najít hodnoty jejích prvků, je algebraický doplněk. Vypočítá se podle vzorce:_ij= (-1) ^i+j * M_ij, kde M je menší. V podstatě - to je další determinant, který může být získán tím, koncepčně odstranit řádku a sloupce, ve kterém je umístěna aktivní prvek. Například, pro tabulku, podle druhého řádu, který je uveden výše v textu, Prvek a₁₁ Algebraický doplněk je prvek a₂₂.

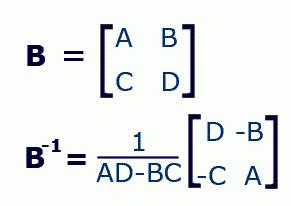
Inverzní matice se nachází ve 3 etapách. V první fázi je určen determinant. V dalším kroku jsou všechny algebraické doplňky, které jsou pak psány v souladu s jejich indexy, výnosem tabulky algebraických doplňků. V závěrečné fázi se získá inverzní matice, jejíž nález se ukončí vynásobením každého algebraického doplnění determinanty.

Nejčastěji používané matice jsouprovádění ekonomických výpočtů. S jejich pomocí můžete snadno a rychle zpracovat velké množství informací. V tomto případě bude konečný výsledek prezentován ve formě vhodné pro vnímání.

Další oblast lidské činnosti v roce 2006které matrice také našly skvělou aplikaci - je modelování 3D obrazů. Tyto nástroje jsou integrovány do moderních balíčků pro implementaci 3D modelů a umožňují návrhářům rychle a přesně vyrábět potřebné výpočty. Nejvýraznějším představitelem těchto systémů je Compass-3D.

Dalším programem, v němž jsou integrovány nástroje pro takové výpočty, je Microsoft Office a konkrétně tabulka aplikace Excel.