Základní typy a příklady cyklických algoritmů

Článek je navržen tak, aby poskytoval základní pojmy jaký je cyklický algoritmus, který je společný jakémukoli programovacímu jazyku a úrovni přípravy programátora.

Koncept algoritmu

Algoritmus je sled akcívyřešit výpočetní a další problémy v konečném počtu kroků. Akce (instrukce) pro provádění algoritmu mohou být prováděny postupně, současně (paralelně) nebo v libovolném pořadí za použití cyklů a přechodových podmínek. Algoritmy se používají nejen v programování, ale i v jiných oblastech činnosti, například v řízení výrobních a obchodních procesů.

Cyklické algoritmy

Algoritmus se říká, že je cyklický, pokud je v němExistují akce nebo skupiny akcí, které je třeba provést více než jednou. Opakované algoritmické akce jsou tělem cyklu. Navíc každý cyklus má podmínku, že ukončení cyklického algoritmu končí.

Druhy cyklických algoritmů

Každý cyklický algoritmus má ve svém složenístav smyčky, tj. např. logický výraz, který definuje kontrola bude prováděna v těle cyklu znovu, nebo cyklus je kompletní. Podle způsobu léčení všechny cyklické algoritmy jsou rozděleny do tří skupin.

Cyklus s předpokladem

V takových cyklických algoritmech je před zpracováním těla smyčky zkontrolována podmínka pokračování, tj. Je potřeba opakovat zpracování smyčky.

Zvažte výstup čísel od -5 do 0 jako příklad cyklických algoritmů s předpokladem:

Prvky algoritmu:

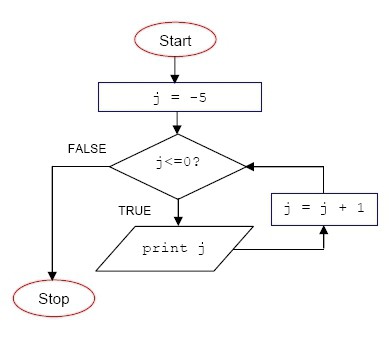
1. Nastavte počáteční hodnotu základní proměnné j na hodnotu -5.
2. Zkontrolujeme stav cyklu. Stav je pozitivní a tělo smyčky se poprvé spustí.
3. Dále přidáme 1 k proměnné j, znovu zkontrolujeme stav cyklu.
4. Smyčka pokračuje v chodu, pokud je hodnota j menší nebo rovna nule, jinak opustíme smyčku na větve FALSE

Cyklus s postcondition

Kontrola stavu se provádí po prvním zpracování těla smyčky a ovládá výstup z ní.

Podívejme se na výpočet součtu od 1 do čísla n jako příklad cyklických algoritmů, ve kterých se použije postcondition:

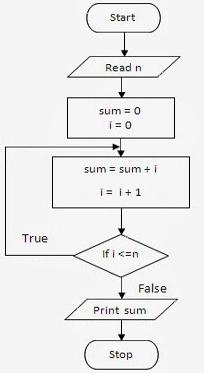
1. Zadáme konečné číslo výpočtu součtu n a nastavíme nulové počáteční hodnoty součtu celkové sumy a počitadla cyklu i.
2. Smyčka se provádí před první kontrolou stavu.
3. Zkontrolujeme stav smyčky, tj. Hodnota čítače i je menší nebo rovna n.
4. Pokud je výsledek stavu kladný, opakujeme smyčku, jinak ukončíme smyčku a vytiskneme část na displeji nebo vytiskneme.

Nepodmíněný cyklus

Obvykle se používá v algoritmech, kdy je požadovaný počet smyček poprvé znám, a je velmi často používán při práci s maticemi.

Tento algoritmus obsahuje tři povinné prvky:

1. Počáteční hodnota, která se nazývá parametr smyčky, protože se tato proměnná změní po každém provedení cyklu a určí čas jeho dokončení.
2. Hodnota, se kterou smyčka končí.
3. Krok cyklu.

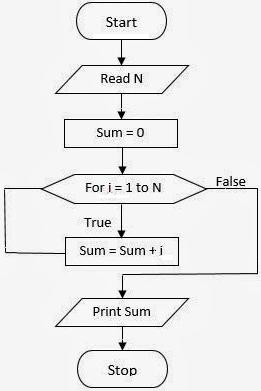
V každém kroku to program ověřujeZda je počáteční hodnota konečná. A pokud ano, cyklus končí. Jinak přidáme velikost kroku k počáteční hodnotě a cyklus se opakuje. Je třeba speciálně poznamenat, že jakýkoli nepodmíněný cyklus může být nahrazen podmíněným cyklem s předběžnou nebo pozdější podmínkou.

Při sestavování cyklických algoritmů,dodržovat dvě závazné podmínky. Za prvé, pro ukončení smyčky je nutné, aby obsah těla ovlivňoval post nebo předpoklad, jinak můžeme skončit nekonečnou smyčkou. Pro některé softwarové úlohy se však používají takové cykly. Jako příklad cyklických algoritmů, které běží na dobu neurčitou, můžeme citovat operační systém Windows, kde se pro určení uživatelských akcí používá nekonečný cyklus dotazování myší. Za druhé, proměnné předané smyčce musí poskytnout alespoň jedno provedení.

Výpočet faktoriální

Pro zpevnění čtení uvádíme příkladcyklické algoritmy pro výpočet faktoriálu celého čísla. Výše uvedený příklad je smyčka s předpokladem, ale je možné implementovat jakýkoli druh cyklického algoritmu.

• Vstup: data jsou celé číslo, pro které je definován faktor.
• Systémové proměnné: parametr cyklu i, který odebírá hodnoty od 1 do dat v kroku 1.
• Výsledek: variabilní faktor je faktoriál číselných dat, který je součtem celých čísel od 1 do dat.

Zvažte algoritmus v krocích:

1. Algoritmus obdržela číselná data, pro která je nutné vypočítat faktoriál.
2. Variabilní faktor, ve kterém bude uložen konečný výsledek, má hodnotu 1.
3. Uspořádáme smyčku s parametrem i a počáteční hodnotou 1. Konečná hodnota je počáteční číselná data. Jakmile je hodnota čítače i větší, smyčka končí.
4. Vykonává se cyklus faktoriálního výpočtu - násobí se aktuální hodnoty faktoriálu a čítače i.
5. K hodnotě čítače přidáme jednotku, zkontrolujte stav smyčky a pokud je výsledek kladný, ukončíme ji.
6. Po poslední iteraci smyčky hodnota faktoriálních dat! zůstává ve faktorech a je zobrazen nebo vytištěn.
</ ol </ p>