Regrese v aplikaci Excel: rovnice, příklady. Lineární regrese

Regresní analýza je statistická metodaStudie, která ukazuje závislost parametru na jedné nebo více nezávislých proměnných. V předkompilované éře bylo jeho použití poměrně obtížné, zvláště když se jednalo o velké množství dat. Dnes, když se učíte stavět regresi v aplikaci Excel, můžete vyřešit složité statistické problémy během několika minut. Níže jsou uvedeny konkrétní příklady z oblasti ekonomie.

Typy regrese

Samotný koncept byl zaveden do matematiky Francisem Galtonem v roce 1886. Regrese se děje:

lineární;
parabolický;
mocenské právo;
exponenciální;
hyperbolická;
orientační;
logaritmický.

Příklad 1

Podívejme se na problém určení závislosti počtu členů na kolektivu v důchodu od průměrné mzdy v 6 průmyslových podnicích.

Úkol. Šest podniků analyzovalo průměrný měsíční plat a počet zaměstnanců, kteří opustili svou vlastní vůli. V tabulkové podobě máme:

	A	B	C
1	X	Počet odstoupil	Plat
2	X	y	30000 rublů
3	1	60	35 000 rublů
4	2	35	40000 rublů
5	3	20	45 000 rublů
6	4	20	50 000 rublů
7	5	15	55 000 rublů
8	6	15	60000 rublů

Pro problém určení závislosti počtu zaměstnanců, kteří odešli na průměrnou mzdu u 6 podniků, má regresní model podobu rovnice Y = a₀ + a₁x₁ + ... + a_kx_k, kde x_i - ovlivňování proměnných, a_i - koeficienty regrese a k - počet faktorů.

Pro tento úkol je Y ukazatelem zaměstnanců, kteří odešli, a faktorem, který ovlivňuje, je plat, kterou označuje X.

Použití procesoru tabulky aplikace Excel

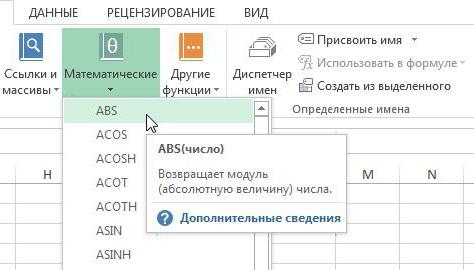
Je třeba předcházet analýzu regrese v aplikaci Excelpoužití vestavěných funkcí k dostupným datům. Pro tyto účely je však lepší použít velmi užitečný doplněk "Analysis package". Chcete-li ji aktivovat, potřebujete:

Na kartě "Soubor" přejděte do sekce "Možnosti".
v otevřeném okně vyberte řádek "Doplňky";
Klikněte na tlačítko "Přejít", které je umístěno vpravo od řádku "Řízení".
Zaškrtněte políčko vedle názvu "Balíček analýzy" a potvrďte své akce klepnutím na tlačítko "Ok".

Pokud je provedena správně, pravé tlačítko se zobrazí na pravé straně karty Údaje umístěné nad tabulkou aplikace Excel.

Lineární regrese v aplikaci Excel

Nyní, když máme k dispozici všechny potřebné virtuální nástroje k provedení ekonometrických výpočtů, můžeme začít řešit náš problém. Postupujte takto:

klikněte na tlačítko "Analýza dat";
v otevřeném okně klikněte na tlačítko "Regrese";
na kartě, která se objeví, zadáme rozsah hodnot pro Y (počet zaměstnanců, kteří odešli) a X (jejich plat);
naše akce potvrdíme klepnutím na tlačítko "Ok".

V důsledku toho se program automaticky vyplnínová regresní analýza dat v procesorech tabulkových tabulek. Dávejte pozor! V aplikaci Excel máte možnost nezávisle nastavit místo, které preferujete pro tento účel. Mohlo by to být například stejný list jako hodnoty Y a X nebo dokonce i nová kniha speciálně navržená pro ukládání takových dat.

Analýza výsledků regrese pro čtvereček R

V aplikaci Excel jsou data získaná během zpracování dat z příkladu v podobě:

Především je třeba věnovat pozornosthodnota čtverce R. Je to koeficient určení. V tomto příkladu je R-kvadrát = 0,755 (75,5%), m. E. Vypočtené parametry modelu vysvětlit vztah mezi parametry zvažovaných 75,5%. Čím vyšší je hodnota koeficientu určení, zvolený model je považován za použitelnější pro konkrétní úkol. Předpokládá se, že správně popisuje skutečnou situaci s hodnotou R-čtverce vyšší než 0,8. V případě, že R-square <0,5, pak regresní analýza v Excelu nelze považovat za přiměřené.

Analýza koeficientů

Číslo 64.1428 ukazuje, jaká bude hodnota Y,pokud jsou všechny proměnné xi v uvažovaném modelu vynulovány. Jinými slovy, lze argumentovat, že hodnota analyzovaného parametru je ovlivněna jinými faktory, které nejsou popsány v konkrétním modelu.

Následující koeficient je -0.166285, který se nachází vB18 buněk ukazuje vliv hmotnosti proměnné X Y. To znamená, že průměrný plat zaměstnanců v rámci modelu ovlivňuje počet odstoupení od hmotnosti -0.16285, t. E. rozsah jejího dopadu je poměrně malý. Znak "-" označuje, že koeficient má zápornou hodnotu. Je to zřejmé, protože každý ví, že čím vyšší je plat v podniku, tím méně lidí vyjadřuje touhu ukončit pracovní smlouvu nebo odjet.

Více regrese

Tímto termínem rozumíme rovnici spojení s několika nezávislými proměnnými tvaru:

y = f (x₁+ x₂+ ... x_m) + ε, kde y je výsledný atribut (závislá proměnná) a x₁, x₂, ... x_m- to jsou znaky-faktory (nezávislé proměnné).

Vyhodnocení parametrů

Pro vícenásobnou regresi (MP) se provádí metodou nejmenších čtverců (OLS). Pro lineární rovnice tvaru Y = a + b₁x₁ + ... + b_mx_m+ ε stavíme systém normálních rovnic (viz níže)

Chcete-li porozumět principu metody, zvažte dvoufaktorový případ. Pak máme situaci popsanou vzorcem

Proto získáme:

kde σ je odchylka odpovídající charakteristiky odrážející se v indexu.

OLS je použitelný pro rovnici MP v standardní měřítku. V tomto případě získáme rovnici:

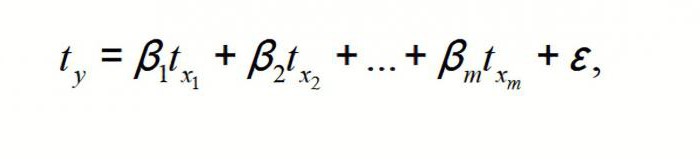
ve kterém t_y, t_x_{1, ...}t_xm-standardizované proměnné, pro které jsou průměry 0; b_i - standardizované regresní koeficienty a směrodatná odchylka je 1.

Všimněte si, že všechny β_iV tomto případě jsou uvedeny jako normalizované acentralizované, takže jejich srovnání mezi sebou je považováno za správné a přípustné. Kromě toho je obvyklé vyčíslovat faktory, které vylučují ty, které mají nejnižší hodnoty βi.

Problém pomocí rovnice lineární regrese

Předpokládejme, že v posledních 8 měsících je tabulka cenové dynamiky konkrétní komodity N. Je třeba rozhodnout o účelnosti nákupu své šarže za cenu 1850 rublů za tunu.

	A	B	C
1	měsíčního čísla	název měsíce	cena komodity N
2	1	Leden	1750 rublů za tunu
3	2	Únor	1755 rublů za tunu
4	3	Března	1767 rublů za tunu
5	4	duben	1760 rublů za tunu
6	5	Květen	1770 rublů na tunu
7	6	červen	1790 rublů na tunu
8	7	červenec	1810 rublů na tunu
9	8	srpen	1840 rublů na tunu

Řešení tohoto problému v stolním procesoruPro použití již známého nástroje "Analýza dat" se vyžaduje "Excel". Poté vyberte sekci Regrese a zadejte parametry. Je třeba si uvědomit, že v poli "Vstupní interval Y" je třeba zadat rozsah hodnot pro závislou proměnnou (v tomto případě ceny zboží v konkrétních měsících roku) a v "Intervalu vstupu X" - pro nezávislé číslo měsíce. Potvrďte akci kliknutím na tlačítko "Ok". Na novém listu (pokud je to uvedeno) dostaneme data pro regresi.

Stavíme na nich lineární rovnici tvaru y = ax + b, kdeparametry a a b jsou koeficienty řádku s názvem čísla měsíce a koeficienty a řádky "Y-křižovatka" z listu s výsledky regresní analýzy. Proto je rovnice lineární regrese (VR) pro problém 3 napsána jako:

Cena komodity N = 11,714 * číslo měsíce + 1727,54.

nebo v algebraické notaci

y = 11,714 x + 1727,54

Analýza výsledků

Rozhodnout, zda výsledná rovnicelineární regrese, koeficienty vícenásobné korelace (KMC) a stanovení, stejně jako kritérium Fishera a Studentův test. V tabulce aplikace Excel s výsledky regrese se objevují pod jmény několika R, R-squared, F-statistik a t-statistiky.

KMK R umožňuje odhadnout těsnostPravděpodobnostní vztah mezi nezávislými a závislými proměnnými. Jeho vysoká hodnota naznačuje relativně silný vztah mezi proměnnými "Číslo měsíce" a "Cena zboží N v rublech na 1 tunu". Nicméně povaha tohoto vztahu zůstává neznáma.

Čtverec koeficientu určení R²(RI) je číselná charakteristikapodílu na celkovém rozpětí a ukazuje rozptyl jaké části experimentálních dat, tj. Hodnoty závislé proměnné odpovídají lineární regresní rovnici. V daném problému je tato hodnota 84,8%, tj. Statistické údaje jsou popsány s vysokou mírou přesnosti přijatým SD.

F-statistická, také nazývaná Fisherova kritéria, se používá k posouzení významu lineární závislosti, vyvrácení nebo potvrzení hypotézy její existence.

Hodnota t-statistiky (Studentův test) pomáhá vyhodnotit význam koeficientu pro neznámé nebo volné termíny lineární závislosti. Pokud hodnota t-test> t_cr, potom je odmítnuta hypotéza nevýznamnosti volného termínu lineární rovnice.

Ve zkoumaném problému pro volný termínprostřednictvím „Excel“ nástroj bylo zjištěno, že t = 169,20903 a p = 2,89E-12, t. j. mají nulovou pravděpodobnost, že věrný bude odmítnuta hypotézu bezvýznamnost volné období. Pro koeficient s neznámým t = 5.79405 a p = 0.001158. Jinými slovy, pravděpodobnost, že zamítnuta správná hypotéza bezvýznamnosti koeficientu pro neznámého, je 0,12%.

Tak lze argumentovat, že výsledná lineární regresní rovnice je adekvátní.

Problém účelnosti nákupu bloku akcií

Více regrese v aplikaci Excel se provádí pomocí stejného nástroje "Analýza dat". Uvažujme o konkrétním aplikovaném problému.

Správní společnost "NNN" by měla rozhodnouto účelnosti nákupu 20% podílu v MMM. Náklady na balíček (SP) činí 70 milionů amerických dolarů. Specialisté z "NNN" shromáždili údaje o podobných transakcích. Bylo rozhodnuto vyhodnotit hodnotu podílu v těchto parametrech, vyjádřených v milionech dolarů, jako:

splatné účty (VK);
objem ročního obratu (VO);
pohledávky (VD);
hodnoty dlouhodobých aktiv (SOF).

Kromě toho je v tisících amerických dolarů používán parametr nedoplatků na mzdy podniku (V3 P).

Řešení pomocí tabulky aplikace Excel

Nejprve je třeba vytvořit tabulku vstupních dat. Má následující formu:

Další:

Zavolejte okno "Analýza dat";
vyberte sekci "Regrese";
V poli "Vstupní interval Y" zadejte rozsah hodnot závislých proměnných ze sloupce G;
klikněte na ikonu s červenou šipkou napravo od okna "Vstupní interval X" a vyberte rozsah všech hodnot ze sloupců B, C, D, F na listu.

Označte položku "Nový pracovní list" a klikněte na tlačítko "Ok".

Pro tento úkol je získána regresní analýza.

Výsledky studie a závěry

"Sběr" ze zaokrouhlených dat uvedených výše v tabulce tabulky Excel, regresní rovnice:

SP = 0,103 * SOF + 0,541 * VO - 0,031 * VK + 0,405 * VD + 0,691 * VZP - 265,844.

V známější matematické formě může být zapsána jako:

y = 0,103 * x1 + 0,541 * x2 - 0,031 * x3 + 0,405 * x4 + 0,691 * x5 - 265,844

Údaje pro MMM jsou následující:

SOF, USD	VO, USD	VK, USD	VD, USD	VZP, USD	JV, USD
102,5	535,5	45,2	41,5	21,55	64,72

Nahrazujeme je do regresní rovnicečíslo 64,72 milionu amerických dolarů. To znamená, že akcie MMM by neměly být zakoupeny, protože jejich hodnota 70 milionů amerických dolarů je poněkud nadhodnocená.

Jak vidíte, použití tabulkového procesoru Excel a regresní rovnice umožnily informované rozhodnutí o proveditelnosti velmi specifické transakce.

Nyní víte, jaká je regrese. Příklady v programu Excel, které jsou popsány výše, vám pomohou při řešení praktických problémů z oblasti ekonometrie.